|
Question 1143792: find the equation of the circle woth center at (-3,8) and tangent to the line
x-y+5=0
Answer by ikleyn(52798)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
As soon as you find the radius of the circle, you will be in position to write its equation.
The radius of the circle is equal to the distance from the given center to the given line.
To find this distance, use the general formula for the distance from the point (p,q) to the line Ax + By + C = 0
in the coordinate plane
d = 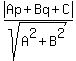 . (1)
In your case A= 1, B= -1, C= 5, p= -3, q= 8.
So from the formula (1), the distance from the point (-3,8) to the line x-y+5 = 0 is
d = . (1)
In your case A= 1, B= -1, C= 5, p= -3, q= 8.
So from the formula (1), the distance from the point (-3,8) to the line x-y+5 = 0 is
d =  = = 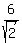 .
Thus the radius of the circle is r = d = .
Thus the radius of the circle is r = d = 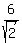 .
Then the standard equation of the circle is .
Then the standard equation of the circle is
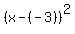 + + 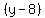 = = 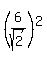 ,
or, equivalently, ,
or, equivalently,
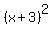 + + 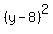 = 18. = 18.
Solved.
---------------
Regarding the basic formula (1), see the lessons
- The distance from a point to a straight line in a coordinate plane
- HOW TO calculate the distance from a point to a straight line in a coordinate plane
- Using formula for the distance from a point to a straight line in a plane to solve word problems
in this site.
/\/\/\/\/\/\/\/
Let me REMIND you that it is commonly accepted among the educated and civilized people to thank for help.
Moreover, expressing gratitude for help is not a "good style" only -- it is MUST.
During weeks, I produce tens first class solutions to visitors, but do not see their expressed gratitude . . .
Do not forget to post your "thanks" to me through the "Thank you" (or "student comments") window.
Otherwise, I will think that I work for idiots . . .
|
|
|
| |