|
Question 1143657: Find the equation of the circle that passes through the points of intersection of the circles x²+y²=2x, x²+y²=2y and has its center on the line y=2.
Found 2 solutions by ikleyn, Alan3354:
Answer by ikleyn(52799)   (Show Source):
You can put this solution on YOUR website! .
(1) Since the left sides are identical in given equations of the circles, their right sides are equal for intersection points
x = y.
(2) Substituting x=y into the circles equations gives
x^2 + x^2 = 2x ====> 2x^2 = 2x ====> 2x^2 - 2x = 0 ====> 2x(x-1) = 0.
The roots are x= 1 and x= 0, so the intersection points are A=(1,1) and B=(0,0).
(3) The center of the third circle lies on the perpendicular bisector to the segment AB.
An equation of this perpendicular bisector is y-0.5 = -(x-0.5) = -x + 0.5.
(4) At the same time, the center of the third circle lies on the line y= 2.
So, the center of the third circle is at
2 - 0.5 = -x + 0.5,
which implies x= -1.
Thus the center of the third circle is the point P = (-1,2).
The radius of the third circle is the distance of the point P from the origin (0,0), i.e.  =  =  .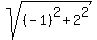
(5) Thus the equation of the circle under the question is
 +  =  ,
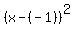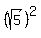or, equivalently,
 + = 5. ANSWER
Answer by Alan3354(69443)  (Show Source):
You can put this solution on YOUR website! Find the equation of the circle that passes through the points of intersection of the circles x²+y²=2x, x²+y²=2y and has its center on the line y=2.
---------------------
Find the 2 points of intersection.
They're (0,0) and (1,1)
=============================
The center is on the perpendicular bisector of y=x thru the 2 points ---> slope = -1 thru the point (1/2,1/2)
---> y - 0.5 = -1*(x - 0.5)
y = -x + 1
==============
The center is the intersection of y = -x + 1 and y = 2
2 = -x + 1
x = -1
y = 2
---> the center is (-1,2)
--------------------
r = the distance from (-1,2) to either point.
r = sqrt(5)
The circle is 
|
|
|
| |
