|
Question 1142038: Determine which of the conic sections is represented.
4x² + 14xy + 5y² + 18x − 6y + 30 = 0
Found 2 solutions by Alan3354, ikleyn:
Answer by Alan3354(69443)   (Show Source):
You can put this solution on YOUR website! Determine which of the conic sections is represented.
4x² + 14xy + 5y² + 18x − 6y + 30 = 0
===============
It's a parabola.
I graphed it.
Determining the answer by other means is tough.
IDK how to do that, but I would be interested in learning.
=========================
I don't pretend to know everything.
I can do LaPlace transforms, Fourier series, and Heavyside expansions, tho.
IDK how to find LaGrange points of an orbit.
-------------
Someday knowing all that might be useful, but not so far.
Answer by ikleyn(52799)  (Show Source):
You can put this solution on YOUR website! .
Your conic section is presented by equation
4x² + 14xy + 5y² + 18x − 6y + 30 = 0.
The equation has a mixed term xy -- therefore, it may happen that the standard high school knowledge is not enough
to answer the question.
But the answer does exist in Analytic Geometry.
To determine the type of the conic section, calculate the discriminant
d = B^2 - 4*A*C,
where B = 14 is the coefficient at the "xy"-term;
A = 4 is the coefficient at the "x^2"-term;
C = 5 is the coefficient at the "y^2"-term.
In your case the discriminant d = 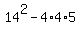 = 116 is a positive real number.
It means that the conic section is a HYPERBOLA.
For details, read your textbook or learn from the universal source WIKIPEDIA - see Wikipedia article
https://en.wikipedia.org/wiki/Conic_section
https://en.wikipedia.org/wiki/Conic_section
|
|
|
| |
