Question 1136330: Find the equation in standard form of the hyperbola that has foci at (8, 1)(-8, 1) and
transverse axis with length 14.
Answer by MathLover1(20850)   (Show Source):
You can put this solution on YOUR website! Find the equation in standard form of the hyperbola that has
foci at ( ,  ) , ( , )
and transverse axis with length 
The standard form of a hyperbola that opens sideways is
For the hyperbola that opens up and down, it is
In both cases, the center of the hyperbola is given by ( ,  ).
The vertices are  spaces away from the center.
The "foci" of an hyperbola are "inside" each branch, and each focus is located some fixed distance  from the center.
The endpoints of the transverse axis are called the vertices of the hyperbola.
The distance between the vertices is  . The distance between the foci is  .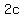
if foci at (, ) , (, ) , the distance between is  , then
if transverse axis with length , means distance between vertices is
 ->
and vertices are at ( ,  ) , ( , )
and its midpoint is the center of the hyperbola => which is at (, )
find 
|
|
|
