|
Question 1132760: An arch in the shape of a parabola has height 630ft and width 630ft. How wide is the arch 300 ft up?
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! An arch in the shape of a parabola has height 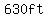 and width and width 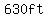 . How wide is the arch . How wide is the arch  up? up?
The width of the bridge is 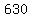 feet so the parabola crosses the x-axis with x-coordinates ± feet so the parabola crosses the x-axis with x-coordinates ± 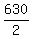 = ± = ± 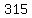
=> x-intercepts are at (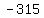 , , ) and ( ) and (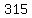 , , ) )
Assume that it stands on the x axis, that it is symmetric with respect to the y-axis, and that it is 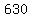 feet wide at the base and feet wide at the base and 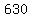 feet high at the feet high at the  . .
Then the maximum height occurs at  ; so, the vertex of the parabola is =>( ; so, the vertex of the parabola is =>( , ,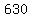 ) )
Since the curve is a parabola which opens downward its equation can be written

since  and and 


x-intercepts are at (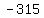 , , ), use x-intercept to find ), use x-intercept to find 





and, equation is

to find how wide is the arch  up, substitute up, substitute 








 = ± = ± 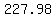
the arch  ft have intercepts at ( ft have intercepts at (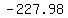 , , ) and ( ) and (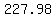 , , ), so width will be the distance from ), so width will be the distance from  to to  which is which is  ft ft
answer: the arch  ft up is ft up is 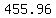 ft wide ft wide
|
|
|
| |