Question 1121763: how to find a b and c, eccentricity, directrix, sf, gf endpoints of LR, LR B, V(vertex) and foci
9x^2 + 4y^2 - 24y -72 + 144 = 0
(ellipse)
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
 ...-> I guess you got ...-> I guess you got 











major axis is vertical, so compare to  , you see that , you see that


 => =>
 => =>
eccentricity : 
first find  : :





eccentricity: 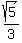 ≈ ≈ 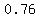
center: ( , ,  ) )
foci : ( , ,  ) and ( ) and ( , , 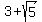 ) )
or ≈ ( , , 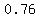 ) and ( ) and ( , , 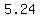 ) )
vertices:( , ,  ) and ( ) and ( , , ) )
covertices: ( , ,  ) and ( ) and ( , ,  ) )
|
|
|