|
Question 1114072: What are the steps to find the equation of an ellipse with foci (0,-3) and (0,3); the point (8,3) on the ellipse?
Answer by ikleyn(52802)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
1. First of all, you see that the foci lie in vertical line x= 0 and the center of the ellipse,
which is the midpoint between the foci, coincides with the origin of the coordinate system (0,0).
So, the ellipse is centered at (0,0).
2. Let F1 = (0,-3) and F2 = (0,3) be the names of the foci.
The distance from F1 to the point (8,3) at the ellipse is 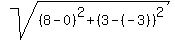 = =  = 10 units.
The distance from F2 to the point (8,3) at the ellipse is = 10 units.
The distance from F2 to the point (8,3) at the ellipse is 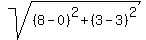 = =  = 8 units.
The sum of these distances is 18 units.
According to the definition of an ellipse, the sum of distances from foci to any point on the ellipse is constant.
So, for our ellipse the sum of distances from foci to any points on the ellipse is 18 units.
3. Let "a" and "b" be semi-major and semi-minor axes of our ellipse, respectively
(a" is along the vertical axis and "b" is along the horizontal axis).
At given conditions, the point B = (b,0) lies at the ellipse; indeed, it is the co-vertice point of the ellipse.
Due to symmetry, the distances from F1 and F2 to the point B are the same, and each of the distances is half of 18, i.e. 9 units.
So the three points F1, (0,0) and B are vertices of the right-angled triangle with the hypotenuse of 9 units long and one of the leg 3 units long
(from F1 to the center of the ellipse).
Hence, the other leg is = 8 units.
The sum of these distances is 18 units.
According to the definition of an ellipse, the sum of distances from foci to any point on the ellipse is constant.
So, for our ellipse the sum of distances from foci to any points on the ellipse is 18 units.
3. Let "a" and "b" be semi-major and semi-minor axes of our ellipse, respectively
(a" is along the vertical axis and "b" is along the horizontal axis).
At given conditions, the point B = (b,0) lies at the ellipse; indeed, it is the co-vertice point of the ellipse.
Due to symmetry, the distances from F1 and F2 to the point B are the same, and each of the distances is half of 18, i.e. 9 units.
So the three points F1, (0,0) and B are vertices of the right-angled triangle with the hypotenuse of 9 units long and one of the leg 3 units long
(from F1 to the center of the ellipse).
Hence, the other leg is  = =  = =  .
This leg is nothing else as the minor semi-axis b. Thus b = .
This leg is nothing else as the minor semi-axis b. Thus b =  .
4. Now for our ellipse we know the linear eccentricity c = 3 units and the minor semi-axis b = .
4. Now for our ellipse we know the linear eccentricity c = 3 units and the minor semi-axis b =  .
Then the major semi-axis a = .
Then the major semi-axis a =  = = 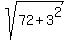 = = 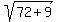 = = 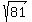 = 9.
5. Having this, we can write the equation of our ellipse: = 9.
5. Having this, we can write the equation of our ellipse:
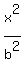 + + 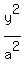 = 1, or = 1, or 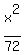 + + 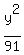 = 1. (1) = 1. (1)
You may check that the given point (8,3) belongs to the ellipse, i.e. satisfies equation (1).
|
|
|
| |