|
Question 1110815: find the area bounded by the curve y^2=9x and its latus rectum
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! 
In this case, the latus rectum is part of the line  .
Parabola, focus, directrix and latus rectum look like this
 The area we want is the area between the red/green curve and the blue latus rectum.
ONE WAY:
As the halves above and below the x-axis are symmetrical, we can calculate that area as twice the area above the x-axis.
When we only consider that half, with  ,
is equivalent to  , so  
As the antiderivative is  ,
that area is
 .
ALTERNATIVELY,
you could do like you may have to do in other cases and interchange variables
(or take x as a function of y).
is equivalent to  taking x as a function of y.
That curve and  intersect at  .
In other words, the endpoints of the latus rectum are the points with
 .
We can calculate the area between the functions of  ,
and ,
in the interval from  to  as
 ,
or better yet 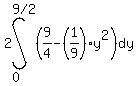as
 . As  ,
the area would be calculated as
   .
|
|
|
| |
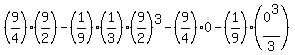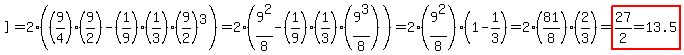