SOLUTION: ellipse and hyperbola Find the coordinates of the vertices 4y^2 - 38x^2 = 144

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: ellipse and hyperbola Find the coordinates of the vertices 4y^2 - 38x^2 = 144      Log On


   

Question 1108705: ellipse and hyperbola
Find the coordinates of the vertices
4y^2 - 38x^2 = 144
Answer by ikleyn(52802) About Me  (Show Source):
You can put this solution on YOUR website!
.
It is a hyperbola with y-axis as a real axis.


The center is at (0,0), the origin of the coordinate plane.


The vertices are the points of the curve lying at y-axis  x= 0.


So, substitute x= 0 into the equation and get  4y^2 = 144,


which implies  y^2 = 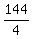144%2F4 = 36,  y = +/-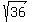sqrt%2836%29 = +/-6.


So the vertices are  (0,6)  and  (0,-6).

-----------
See the lesson
    - Hyperbola definition, canonical equation, characteristic points and elements
in this site.