|
Question 1092209: C(23,-1), internally tangent to x^2+y^2-34x-14y+313=0. FIND THE EQUATION OF THE CIRCLE ( This is a harder case, please answer w/ complete solution)
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! If one circle is tangent to another,
the radii at the point of tangency are on the same straight line.
If two circles are internally tangent,
they are tangent and one is inside the other.
We should start by figuring out the center and radius of the circle with equation
 . .
I would do it by transforming the equation to one that tells me the radius and center.







That last equation is obviously the equation of the circle
centered at 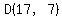 with radius with radius  . .
So, that circle, with its center, and point 
look like this:
 . .
A circle centered at  , ,
and internally tangent to the circle whose equation was given
will be the big red circle below, wit the red radius shown below.
 . .
The radius of the big red circle is
the radius of the smaller blue circle
plus the distance between circle centers  and and 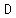 , ,
The distance between  and and 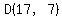 is is
 . .
So, the radius of the big red circle is
 . .
Therefore, the equation of the big red circle is
 or or 
or if you want you can transform the equation above to
 , ,  and and 
|
|
|
| |