Question 1092157: Find the equation of the cus of the point if its distance from R(-4,1) is always one-half its distance from E(3,2)
Answer by ikleyn(52799)   (Show Source):
You can put this solution on YOUR website! .
Find the equation of the  locus of the  points if its distance from R(-4,1) is always one-half its distance from E(3,2)
~~~~~~~~~~~~~~~~~~~~~~~~~
Hello,
it seems clear to me that the problem you sent in your post is above the average school Math level.
It is the Math circle level or collection of advanced problems for preparing to Math Olimpiads.
So, I will assume that your level does correspond to the problem's level.
Therefore, instead of solving your problem "as is", I will place here the solution to other, very similar problem.
Find the locus of points P(x,y) such that the distance from P to (3,0) is twice its distance to (1,0).
Solution
Let (x,y) be the point of this locus.
Then
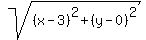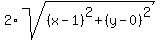 =  . (1)
The left side is the distance from (x,y) to the point (3,0).
The right side is the doubled distance from (x,y) to the point (1,0).
Now square both sides of (1). You will get
 =  .
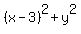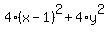Simplify:
 =  ,
 =  ,
 =  ,
 =  ,
 =  ,
=  .
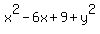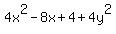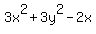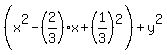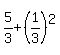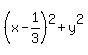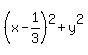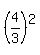It is the equation of the circle of the radius  with the center at the point ( , ).
Answer. The locus under the question is the circle of the radius with the center at the point (,).
Circle =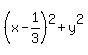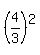
-------------
Having this solution, you will be able to adopt it to your case.
In response, may I ask you to disclose the source of your problem, if it is not a secret ?
You may answer to me through the "Thank you" note.
It would be also interesting to me, whether my solution did help you to complete YOUR problem.
If you will send the message to me through the TY note, do not forget to refer to the problem's ID number 1092157.
Thank you.
------------------
Now I can sign this work proudly: IKleyn, MekhMat MGU (= MSU) 1965/70, PhD in Physics and Mathematics.
|
|
|
