|
Question 1091793: Parabola
The antenna of a radio telescope is paraboloid measuring 81 feet across with depth of 16 feet. Determine, to the nearest tenth of a foot, the distance from the vertex to the focus of this antenna.
Please help. Thank you
Answer by ikleyn(52798)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The antenna of a radio telescope is paraboloid measuring 81 feet across with depth of 16 feet.
Determine, to the nearest tenth of a foot, the distance from the vertex to the focus of this antenna.
~~~~~~~~~~~~~~~~~~~~~~~
If you read the lesson
- Parabola definition, canonical equation, characteristic points and elements
in this site, you will learn that if you write the canonical equation of a parabola in the form
y = 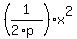 , (1)
then the distance from the parabola's vertex (0,0) to the parabola's focus (focal distance) is , (1)
then the distance from the parabola's vertex (0,0) to the parabola's focus (focal distance) is  .
So, our nearest task is to present the equation of our parabola in the form (1).
For it, substitute y = 16 (depth in feet) and x = .
So, our nearest task is to present the equation of our parabola in the form (1).
For it, substitute y = 16 (depth in feet) and x =  into equation (1). You will get then
16 = into equation (1). You will get then
16 = 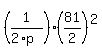 , or 2p = , or 2p = 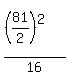 = = 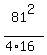 .
Then p = .
Then p = 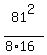 = 51.258.
Thus the focal distance is = 51.258.
Thus the focal distance is  = =  = 25.629 ft. = 25.629 ft.
Answer. The focal distance is 25.629 ft.
-----------------------
I have a gift for you.
-----------------------
The gift is this free of charge online textbook in ALGEBRA-II in this site
ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this online textbook under the topic
"Conic sections: Parabolas. Definition, major elements and properties. Solved problems".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
|
|
|
| |