Question 1091493: Graph each ellipse and clearly indicate the center, foci, vertices, and co-vertices
x^2/16 - x/4 + y^2/9 + 4y/9 = 11/16
PS This is on fractions!! Thank you!'
Found 3 solutions by Alan3354, MathLover1, KMST:
Answer by Alan3354(69443)   (Show Source): (Show Source):
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
 ..........complete squares ..........complete squares










-> and and  , so the center is at ( , so the center is at ( , ,  ) )
semi-major axis length:
 ≈ ≈ 
semi-minor axis length: ≈ ≈





foci: (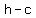 , ,  ) =( ) =(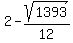 , ,  ) ≈ ( ) ≈ (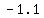 , ,  ) )
and
foci :(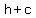 , ,  ) =( ) =(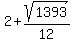 , , ) ≈ ( ) ≈ ( , , ) )
vertices:
The vertices are  units above and below the center, at units above and below the center, at
( , ,  ) ≈ ( ) ≈ ( , ,  ) )
and
(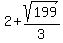 , ,  ) ≈ ( ) ≈ ( , ,  ) )
The co-vertices are  units to either side of the center, at units to either side of the center, at
(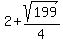 , ,  ) and ( ) and (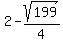 , ,  ) )
Answer by KMST(5328)   (Show Source): (Show Source):
|
|
|