SOLUTION: 1. Graph each parabola and clearly indicate the focus, directrix and endpoints at the latus rectum. y^2 - 8y + 12x - 8 = 0

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: 1. Graph each parabola and clearly indicate the focus, directrix and endpoints at the latus rectum. y^2 - 8y + 12x - 8 = 0      Log On


   

Question 1091389: 1. Graph each parabola and clearly indicate the focus, directrix and endpoints at the latus rectum.
y^2 - 8y + 12x - 8 = 0
Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!

The parabola has a y squared term, so it opens right or left. The vertex form for a parabola that opens right or left is

%28x-h%29+=+%281%2F%284p%29%29%28y-k%29%5E2

In this form, the vertex is (h,k), the length of the latus rectum is |4p|; and p is the distance from the vertex to the directrix and from the vertex to the focus.

So put the equation for your parabola in that form:
y%5E2+-+8y+%2B+12x+-+8+=+0
y%5E2+-+8y+%2B+16+=+-12x+%2B+8+%2B+16 (complete the square in y)
%28y-4%29%5E2+=+-12%28x-2%29
%28x-2%29+=+%28-1%2F12%29%28y-4%29%5E2

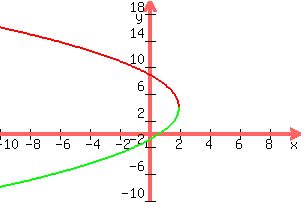
The vertex is (2,4).

4p is -12, so p is -3, indicating that the parabola opens to the left ("in the negative direction").

The directrix is a distance |p| to the right of the vertex; 2+3 = 5, so the directrix is the vertical line x=5.

The focus is a distance |p| to the left of the vertex, at (-1,4).

The length of the latus rectum is 12; since the focus is the midpoint of the latus rectum, the endpoints of the latus rectum are at (-1,10) and (-1,-2).