SOLUTION: How do you find the focus, directrix, and axis for the following equation: 10x-y^2+2y+9=0

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: How do you find the focus, directrix, and axis for the following equation: 10x-y^2+2y+9=0      Log On


   

Question 1089535: How do you find the focus, directrix, and axis for the following equation:
10x-y^2+2y+9=0
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!
10x-y%5E2%2B2y%2B9=0 write in vertex form
10x=y%5E2-2y-9............complete square
10x=%28y%5E2-2y%2Bb%5E2%29-b%5E2-9
10x=%28y%5E2-2y%2B1%5E2%29-1%5E2-9
10x=%28y-1%29%5E2-10
x=%281%2F10%29%28y-1%29%5E2-1
this is sideway parabola
general form is:
x=a%28y-k%29%5E2%2Bh or
+4p%28x-h%29+=+%28y+-k%29%5E2
as you can see, h=-1 and k=1
so, vertex is at (-1,1 )
since a=1%2F10 and 4p=1%2Fa we can find p which is distance of focus from vertex
4p=10
p=5%2F2
focus:
(h%2Bp,k)
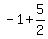=(-1%2B5%2F2,1)
=(3%2F2,1)
directrix: will p=5%2F2 distance from the x coordinate of the vertex
x=+-1-5%2F2
x=+-7%2F2
Every parabola has an axis of symmetry which is the line that runs down its 'center'. This line divides the graph into two perfect halves.If your equation is in vertex form, then the axis of is:
The vertex of this parabola is (-1, 1). The axis of symmetry is at y y=k, so for this example, it is at y+=+1.