Question 1088643: The center of an ellipse is on (-2, -1) and one of its vertex is on (3, -1). It the length of each latus rectum is 4, find the equation of the ellipse, its excentricity and the coordinates of its foci.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
 is an ellipse with center ( is an ellipse with center ( , , ), horizontal axis length ), horizontal axis length  , and vertical axis length , and vertical axis length 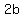 ,vertices are at ( ,vertices are at (  ± ±  , , ), foci is at ( ), foci is at (  ± ±  , ,  ) )
Note that the center is the midpoint of the segment joining the foci.
if the center of an ellipse is on ( , ,  ), we have ), we have  and and 
vertices are at (  ± ±  , , )=( )=( , ,  ) )
=>
=>
foci is at (  ± ±  , ,  )= ( )= (  ± ±  , ,  ) )
so far, your equation is:

the length of each latus rectum is: 
 => => => => => =>

foci is at:
(  ± ± 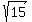 , ,  )=>the coordinates of its foci )=>the coordinates of its foci
( 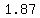 , ,  ) or ( ) or ( 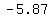 , ,  ) )
your equation is:

 =>the equation of the ellipse =>the equation of the ellipse
and, its eccentricity:  ≈ ≈ 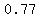
|
|
|