Question 1087740: Please help me solve this hyperbola equation with vertices(5,-3) and (-1,-3) and afocus at (7,-3)
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! hyperbola equation with vertices ( , , ) and ( ) and ( , , ) and a focus at ( ) and a focus at ( , , ) )
the standard form of the equation is: looking at coordinates of vertices, yu have a horizontal hyperbola

center: ( , ,  ) )
vertices: ( ± ±  , , ) )
foci: ( ± ±  , ,  ) )
The vertices are above and below each other, so the center, foci, and vertices lie on a vertical line paralleling the y-axis
The center is 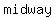 between the two vertices, so if vertices at ( between the two vertices, so if vertices at ( , , ) and ( ) and ( , , ) )
( , , )=( )=(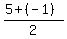 , ,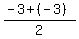 )=( )=( , , ) )
so, 
since vertices:
( ± ± , ,  ) =( ) =( , , )=> )=>
 ± ± = = and since and since  and and  we can find we can find 
so,



since foci:
( ± ±  , ,  )=( )=( , , ) => ) =>
 and since and since  we have we have


since  we can find we can find 




 or or 
so, your equation is:


|
|
|