SOLUTION: 2x^2 + y^2 = 4 the max and min value of 4x + y^2 ?

You are given that  

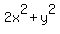 = ,    (1)

and they ask you to find max and min of

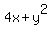.          (2)


    Notice that, due to (1), the domain for x is the set of real numbers   <= x <= .


From (1), you have  = .   Substitute it into (2), replacing  .  You will get

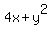 =  =  = (completing the square) =  = .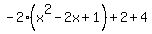


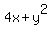Thus the maximum of    is equal to  6  and it is achieved at x = 1.


Or, more precisely, the maximum of 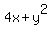   is achieved at the points  (x,y) = (,)  and  (x,y) = (,).


The plot below shows the graph  f(x) =  in the interval  [,].





Plot  f(x) = 



The minimum is at x =  and is equal to 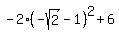 =  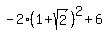= -5.65 (approximately).