Question 1086408: find the volume of the pyramid formed in the octant by the plane 6x+10y+5z-30=0 and the coordinates axes
Answer by KMST(5328)   (Show Source):
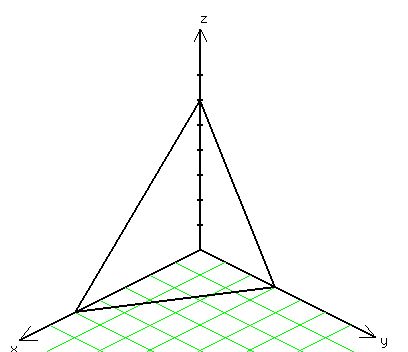
You can put this solution on YOUR website! When y=z=0, you get 6x-30=0 ---> x=5.
When x=z=0, you get 10y-30=0 ---> y=3.
When x=y=0, you get 5z-30=0 ---> z=6.
That plane intersects the coordinate axes at points
(5,0,0) , (0,3,0) , and (0,0,6) .
You could say that the base is the triangle on the x-z plane with vertices (0,0,0) , (5,0,0) , and (0,0,6) ,
and that the altitude is the segment on the y-axis between
(0,0,0) , and (0,3,0) .
So, the area of the base of that pyramid is  ,
and the height is  .
The volume would be
 .
DRAWING ADDED UPON REQUEST:
|
|
|
