Question 1074860: Suppose the point P(x1, y1) is on the hyperbola x^2/a^2-y^2/b^2=1. A tangent is drawn at P, meeting the x-axis at A and the y-axis at B. Also, perpendicular lines are drawn from P to the x- and y-axes, meeting these axes at C and D, respectively. If O denotes the origin, show that:
(a) OA*OC = a^2
(b) OB* OD = b^2.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! There has to be a better way. If so, let me know.
The hyperbola is symmetrical about both axes,
so proving what is requested for the first quadrant portion
should be proof enough.
The hyperbola portion in the first quadrant looks like this:

The coordinates of points C and D are easy.
Since P is 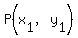 , , 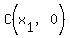 and and 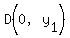 , ,
So  and and 
 <--> <--> 
At 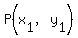 
The derivative of  is is  , so the slope of the tangent at P is , so the slope of the tangent at P is 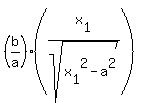 . .
The equation of the tangent, based on point P is
 . .
From that equation we can find the coordinates of points A and B.
For 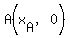 , substituting , substituting  , we can find , we can find  : :
 . .
Solving for 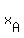 , ,  ---> --->  . .
Substituting the expression found for  , we get , we get
 ---> --->  ---> --->  ---> --->  ---> --->  --> -->  , ,
or in other words  . .
For  , substituting , substituting  , we can find , we can find  : :
 --> -->  --> --> 
Substituting the expression found for  , we get , we get
 --> -->  --> -->  --> -->  --> --> 
Multiplying times  , we get , we get
 --> -->  --> -->  --> --> 
or in other words  . .
|
|
|