SOLUTION: what is the length of the major axis of the ellipse X2+9Y2-2X+18Y+1=0?

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: what is the length of the major axis of the ellipse X2+9Y2-2X+18Y+1=0?      Log On


   

Question 1060958: what is the length of the major axis of the ellipse X2+9Y2-2X+18Y+1=0?
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
x%5E2%2B9y%5E2-2x%2B18y%2B1=0
x%5E2-2x%2B9y%5E2%2B18y=-1
x%5E2-2x%2B1%2B9y%5E2%2B18y%2B9=-1%2B1%2B9
%28x-1%29%5E2%2B9%28y%5E2%2B2y%2B1%29=9
%28x-1%29%5E2%2B9%28y%2B1%29%5E2=9
You can continue to
%28x-1%29%5E2%2F9%2B%28y%2B1%29%5E2=1 ,
but even before that last step, it is obvious that
%28x-1%29%5E2%3C=9 while %28y%2B1%29%5E2%3C=1 ,
so x-1 ranges from -3 to 3 ,
a difference of highlight%286%29 ,
and of course the extreme values of x also have a difference of 6 .
The length of the major axis is highlight%286%29 .


NOTES:
The last two equations show that the ellipse is symmetrical with respect to x=1 and y=-1 , so (1,-1) is the center.
In general, an ellipse can be written in the form
%28x-h%29%5E2%2Fa%5E2%2B%28y-k%29%5E2%2Fb%5E2=1 , or %28x-h%29%5E2%2Fb%5E2%2B%28y-k%29%5E2%2Fa%5E2=1 ,
and once you get to that form,
choosing a and b so that a%3Eb ,
a is the semi-major axis, which is parallel to the x- or y-axis (whatever variable is on to of the a%5E2 ),
b is the semi-minor axis,
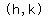%22%28+h+%2C+k+%29%22 is the center,
and you can find the foci knowing that
they are on the major axis, at a distance c to each side of the center, with a%5E2=b%5E2%2Bc%5E2 .