Question 1043408: Find the standard equation,center,foci,asymptotes of 3x^2-2y^2-42x-10y=-64
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the standard equation,center,foci,asymptotes of
 ...group alike terms ...group alike terms
 ..........complete squares ..........complete squares




 ......both sides multiply by ......both sides multiply by 

 .....both sides divide by .....both sides divide by 


 ->hyperbola, the standard equation ->hyperbola, the standard equation


 and and 





so, the center is at ( , , )= ( )= ( , , ) )
foci: since  , the foci will be , the foci will be 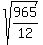 units to either side of the center, and it must be at units to either side of the center, and it must be at
(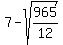 , ,  ) and ( ) and (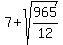 , ,  ) )
or (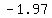 , ,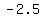 ) and ( ) and (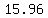 , , 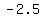 ) )
Since the vertices are  units to either side of the center ( units to either side of the center ( , , )= ( )= ( , , ), then they are at ), then they are at
(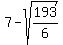 , ,  ) and at ( ) and at (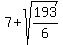 , ,  ) )
or (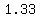 , , 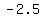 ) and at ( ) and at ( , , 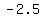 ) )
Since the  went with the went with the  part of the equation, then part of the equation, then  is in the denominator of the slopes of the asymptotes, giving me is in the denominator of the slopes of the asymptotes, giving me  ; so, ; so,  or or  . Keeping in mind that the asymptotes go through the center of the hyperbola, the asymptes are then given by the straight-line equations . Keeping in mind that the asymptotes go through the center of the hyperbola, the asymptes are then given by the straight-line equations
The asymptotes are  , and they are: , and they are:

and


|
|
|