SOLUTION: Find the standard equation of the hyperbola with the center at the origin, vertices at (+- 10, 0) and asymptotes y = +- (3/4)x

Hyperbolas that look like this--->   )( 
have equation:



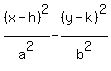Where (h,k) is the center, a is the length of the semi-transverse
axis, and b is the length of the semi-conjugate axis.

The center is the origin so (h,k) = (0,0),
The semi-transverse axis is the line from the center to the
vertex.  This is 10 units long, so a = 10.  So we substitute
in





 

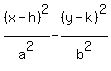
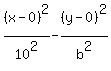
We only need b, the length of the semi-conjugate axis.

The asymptotes are the extended diagonals of the defining rectangle.

The defining rectangle of a hyperbola is the rectangle such that
1. Its dimensions are 2a by 2b, the lengths of the transverse and
conjugate axes.
2. Its diagonals intersect at the center of the hyperbola.
3. The midpoints of two opposite sides of the rectangle are the
vertices of the hyperbola.

The upper right corner of the defining rectangle is the point where
the vertical line x=10 intersects the asymptote with the positive
slope.  

To find the point which is the upper right corner of the defining
rectangle, we solve the system



and get the point 

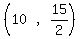So the length of the semi-conjugate axis is .
That is the value of b.  So we substitute b=



 

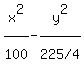That's the standard equation.

Edwin