Question 1043331: Find the standard equation,foci,asymptotes and vertices of 25x^2-39y^2+150x+390y=-225
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! 
The standard equation above tells us that
the center is at (-3,5) ;
the major (or transverse) axis is  ;
the focal distance is  ;
the asymptotes have slopes such that  , and
the y-coordinates of the vertices can be found from
 .
The asymptotes pass through center  ,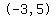
and have slopes such as
--> ,
the equations of the asymptotes (in point-slope form) are
 and  .
Those equations can also be written as
 and
 in slope-intercept form.
Since the foci are on the major axis,
at a distance  from the center,
their y- coordinates are  , or  .
So, one focus is at  ,
and the tother focus is at 
As for the vertices, also on the major axis,
--> --> --->  .
So the vertices are at  and  .
The hyperbola with major axis and foci looks like this:
|
|
|
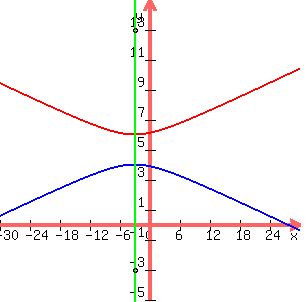
