|
Question 1042705: Find the equation of a hyperbola satisfying the given conditions.
Asymptotes y=1/2x, y=-1/2x; one vertex(4,0)
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The asymptotes of a hyperbola intersect at the center of a hyperbola,
so this hyberbola is centered at the origin,
and that makes life easier.
The equation of a hyperbola centered at the origin is
of the form  , where it is possible to have , where it is possible to have  , ,
or of the form  , where it is not possible to have , where it is not possible to have  . .
(In that equation  and and  are real numbers, are real numbers,
and they are positive by customary definition).
Since vertex (4,0) with  is part of the hyperbola, is part of the hyperbola,
this hyperbola has an equation of the form  . .
Now, al we have to do is find  and and  . .
Substituting the coordinates for the given vertex into  , we see that , we see that
 --> --> ---> ---> --> --> . .
So far, we have {x^2/16- .
As we go farther and farther from the center along the hyperbola,
the terms 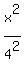 and and  to the left of the equal sign to the left of the equal sign
get so large compared to the  on the other side, on the other side,
that the hyperbola can be approximated by
 <---> <---> <--> <--> . .
Since far from the center the hyperbola "can be approximated" by its asymptotes,
the last two linear equations abovemust be the equations of the asymptotes.
Since the equations given for the asymptotes,
 and and  , ,
must be the same as  and and  , ,
 ---> --->  . .
Putting it all together, tHe equation of the hyperbola is
 or or  . .
|
|
|
| |