SOLUTION: Find the equation of the ellipse center: C(-2,3) major axis is horizontal passes through (1,4) (2,3)

----------------------

So that I won't be doing your homework for you, 
I'll do one exactly like yours with the numbers
changed but with the same step-by-step procedure:

Find the equation of the ellipse 
center: C(-3,4) 
major axis is horizontal
passes through (1,5) (2,4)

All ellipses with center (h,k), semi-major axis length
"a", and semi-minor axis length "b", has equation: 



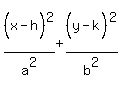Since we know that the center is C(-3,4), we know that
(h,k) = (-3,4), so we can substitute -3 for h and 4 for k.



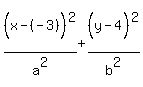or



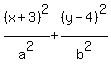We plot the given points. And since the major axis is 
horizontal and the point (2,4) has the same y-coordinate 
as the center, that means that the point (2,4) is the 
right vertex of the ellipse.  So we can sketch it in
like this:



Let's draw in the semi-major axis (in green):



By counting the blocks on the graph paper, we know
that the major axis is 5 units long.  And since "a"
is the length of the major axis, we can substitute 5
for "a" in the equation:



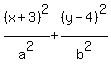and now we have the equation 



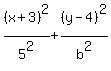or squaring 5:



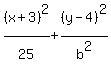All we have left is to find the value of "b²".

To get that we use the point (1,5) that the ellipse
passes through.  We know that when x=1 and y=5, the
equation must be true, so we substitute those
temporarily for the variables x and y:









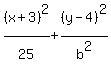
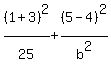
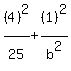
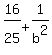We multiply through by the LCD of 25b²



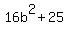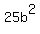Subtract 16b² from both sides:



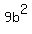Divide both sides by 9



Now we can substitute that for b² and we have the
complete equation for the ellipse:



Now all you have to do is use the above as a model
and do yours step-by-step as the above.

Edwin