|
Question 1042006: I have an algebra 2 question that is about finding an polynomial function that will create three "hills" on a graph. These hills can't be crazy numbers and have to be in the first quadrant. The X-axis is the ground. I asked my teacher and she said that I should compress x^6 and it should work out. However, whenever I graph x^6, it always ends up being a parabola. How can I find the correct equation? Thank you so much for the time and effort :)
Answer by josgarithmetic(39620)   (Show Source): (Show Source):
You can put this solution on YOUR website! x^6 is not a parabola by itself. No compression factor alone will put all of the "hills" of x^6 in the first quadrant. You would want maybe six binomials multiplied, each with an appropriate root which will put x-intercepts to the right of the origin, and then ADD a positive constant of such value that all maxima are ABOVE the x-axis.
You learn about this topic in College Algebra, or something maybe in highschool more advanced than "Intermediate" Algebra.
Let a, b, c, d, e, be positive real numbers.
 ----- no hills, just a line. ----- no hills, just a line.
 ------- again, no hills; just a line. ------- again, no hills; just a line.
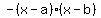 -------- degree two function, would become polynomial; and ONE hill. -------- degree two function, would become polynomial; and ONE hill.
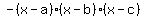 -------degree three function, would become polynomial when multiplied; and ONE hill and ONE valley. -------degree three function, would become polynomial when multiplied; and ONE hill and ONE valley.
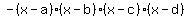 -------this would become polynomial of degree four. Two hills and ONE valleys. -------this would become polynomial of degree four. Two hills and ONE valleys.
 -------polynomial degree five. Two hills and two valleys. -------polynomial degree five. Two hills and two valleys.
What comes next?
|
|
|
| |