|
Question 1039422: P (2p,p^2) is a variable point on the parabola x^2 = 4y. N is the foot of the perpendicular form P to the x axis NR is perpendicular to OP.
a. find the equation of OP
b. find the equation of NR
c. show that the R has coordinates (8p/p^2 +4 , 4p^2/p^2+4)
d. show that the locus R is a circle and state its centre and radius
NEED HELP WITH PART C AND D!!!
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! a. {{OP}}} connect  and and  , ,
so its slope is  and its y-intercept is and its y-intercept is  . .
The equation of  is is 
b. The foot of the perpendicular form  to the x-axis is to the x-axis is
 , and the slope of a line perpendicular to , and the slope of a line perpendicular to  is is
 . .
So, the equation of 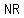 in point-slope form, based on point in point-slope form, based on point  is is

c. you did not tell me where point  is, but from its coordinates, I see that is a point on line is, but from its coordinates, I see that is a point on line  . .
so, R must be the intersecion of NR and OP.
Hence, its coordinates are the solution to
 . .
Using substitution, we start trying to find  from from  . .
Multiplying both sides times  we get we get
 . .




 . .
Then, substituting the value found for  into into  we get we get


d.  is symmetrical with respect to the y-axis, is symmetrical with respect to the y-axis,
because substituting 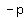 for for  you get point you get point  , ,
the reflection of  across the y-axis. across the y-axis.
Making  gives us the point gives us the point  , which is part of the locus or , which is part of the locus or  . .
All the points  have a non-negative y-coordinate, have a non-negative y-coordinate,
 . .
So the circle should be centered on the y-axis,
pass though  , ,
and otherwise be above the y-axis.
Such a circle has a radius r, and is centered at 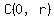 . .
All we need to do is find  . .
The equation of such a circle would be
 <---> <--->  <---> <--->  <---> <--->  . .
Substituting  and and  , we can find , we can find  . .





 ---> --->  . .
The locus of  is a circle of radius is a circle of radius  centered at centered at  . .
NOTES:
The equations to graph that circle: 
can be called parametric equations.
Parametric equations allow us to show a relation that is not a function,
so we can express a relation that graphs as a curve we call a parametric curve.
They are very useful if would be difficult to express with just  and and  . .
A third variable called parameter (in this case  ) is uaed, ) is uaed,
and we define  and and  as functionc of that parameter. as functionc of that parameter.
Many times, we try to "eliminate the parameter",
to get to a relation between just  and and  , ,
be able to understand the relation between  and and  more easily. more easily.
One way to do that is to solve one equation for the parameter,
getting an expression for the parameter in terms of  and and  that can be substituted for the parameter in the other equation for the other variable. that can be substituted for the parameter in the other equation for the other variable.
That would have been complicated in this case, but fortunately we were told it was a circle and all we had to do is prove it and find center and radius.
That made it easier.
Maybe the way I went about it is not the expected way, but it was the easiest way I could figure out.
If you find out about some easier way, let me know.
|
|
|
| |