|
Question 1039314: A.) Write the equation of the parabola in general form completely draw thr graph.
A. V(4,2) , F(2,2)
B. V(5,-1) , F(3,-1)
C. V(4,-4) , y+5=0
B.) Express each in standard form completely draw the graph
D. 4x²+24x-y+3=0
E. y²+4x+6y+17=0
Answer by josgarithmetic(39618)   (Show Source): (Show Source):
You can put this solution on YOUR website! Only doing one of those for you.
C. V(4,-4), y+5=0
This might be vertex and directrix. Solving for y gives y=-5 and no restriction on x for the directrix. This can also be stated as a variable point (x,-5), the directrix.
The focus is on the other side of the vertex. From -4 to -5 is a distance of 1. The focus is therefore 1 unit away from the vertex and this focus must be (4,-3).
Use the definition of a parabola. Find the equation for Distance from (x,y) to (x,-5) is equal to Distance from (x,y) to (4,-3).

Simplify this into whatever form or forms you need.
Find a good demonstration example for how this works, here: deriving equation of parabola for given focus and directrix - video example
-
The finished general form for this example in your list is  . .
Its graph appears like 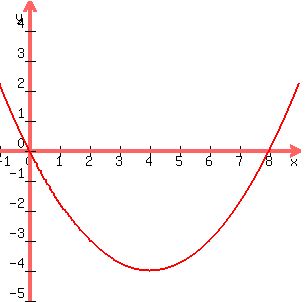 . .
The same channel with that video also has something to explain your last two example equations.
|
|
|
| |