SOLUTION: E is the ellipse with foci at (4,−2) and (4,8) and whose major axis has length 20.

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: E is the ellipse with foci at (4,−2) and (4,8) and whose major axis has length 20.      Log On


   

Question 1037746: E is the ellipse with foci at (4,−2) and (4,8) and whose major axis has length 20.
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
So, that is E, but what is the question?
Write the equation?
Locate vertices and co-vertices?
graph?

Both foci are on the vertical line x=4 ,
so this is an ellipse with foci and vertices on the vertical major axis x=4 .
The center is the midpoint of the segment connecting the foci.
That is point (4,3), with coordinates
x=%284%2B4%29%2F2=4 and y=%28-2%2B8%29%2F2=6%2F2=3
the averages of the foci coordinates.
The focal distance, c , is the distance from one focus to the center:
c=8-3=5 .
Since the major axis has length 20 ,
the semi-major axis is a=20%2F2=10 .
Since the major axis is vertical, the vertices of the ellipse are c=10 units above and below center (4,3), at (4,-7) and (4,13).
The semi-minor axis, b , can be calculated using the relation
a%5E2=b%5E2%2Bc%5E2 .
10%5E2=3%5E2%2Bc%5E2
100-9=b^2}}}
b%5E2=91
b=sqrt%2821%29
The equation of an ellipse with major axis parallel to the y-axis,
center at point (h,k), is
%28x-h%29%5E2%2Fb%5E2%2B%28y-k%29%5E2%2Fa%5E2=1
In this case, with system%28h=4%2Ck=3%2Ca=10%2Cb=sqrt%2891%29%29 ,
the equation is
%28x-a%29%5E2%2F91%2B%28y-3%29%5E2%2F100=1 .
The co-vertices are on the horizontal minor axis,
a distance b=sqrt%2891%29 to the left and rihjt of center (4,3),
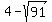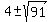at %22%28%224-sqrt%2891%29%22%2C+3+%29%22 and %22%28%224%2B-sqrt%2891%29%22%2C+3+%29%22 .