|
Question 1035086: Distance between the lines 5x+12y-1=0 and 10x+24y+k=0 is 2 then the value of k is
Answer by josgarithmetic(39618)   (Show Source):
You can put this solution on YOUR website! Change this description a little bit. The slopes of both lines must be 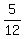 for the description to be meaningful. The two equations of these lines are then 5x+12y-1=0 and 5x+12y+j=0, and you want to find j. The two lines are parallel, and the distance between them is 2.
Here is 5x+12y-1=0 graphed:
The equation can also be stated  .
Choose a convenient point on this line, maybe the x-intercept, ( 1/5 ,0).
You want the other line,  , to be 2 unit away from 5x+12y-1=0; and you can pick either above OR below. Put the equation of the line you wish to find in slope-intercept form, as  .
Summarizing all this, we want distance from to to be equal to 2. To be much more specific, referring to a given or desired point on the first line graphed, we want the distance between ( 1/5, 0 ) and  to be equal to 2.
...
Keep reading and thinking on that.
A general point for the equation of the line you want to find is an ordered pair point ( x, -(5/12)x+j/12 ).
When you have this then use the distance formula to set up the equation necessary to solve for j.
|
|
|
| |
