Question 1033118: Find the vertices, the endpoints of the minor axis, and the foci of the given ellipse.
10x2 + 80x + 7y2 + 42y + 83 = 0
Found 2 solutions by robertb, ikleyn:
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
<==> 
==> 
==> 
==> the center of the ellipse is the point (-4,-3).
Now  and and  ==> ==>  , because for any ellipse, , because for any ellipse,  . .
(Also the major axis is parallel to the y-axis, while the minor axis is parallel to the x-axis.)
==> the vertices are (-4, 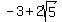 ) and (-4, ) and (-4, 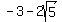 ), ),
the co-vertices are ( ,-3) and ( ,-3) and (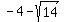 ,-3), ,-3),
while the foci are (-4, 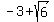 ) and (-4, ) and (-4, 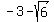 ). ).
Answer by ikleyn(52797)   (Show Source): (Show Source):
|
|
|