|
Question 1033009: Find an equation of the ellipse that satisfies the given conditions:
vertices (+ or - 4, 0), contains the point (2,1)
Answer by ikleyn(52797)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find an equation of the ellipse that satisfies the given conditions:
vertices (+ or - 4, 0), contains the point (2,1)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
I assume that you are familiar with the material of the lesson Ellipse definition, canonical equation, characteristic points and elements
in this site. Surely, you may learn it from other sources. But if you are not familiar with it, I recommend you to read this lesson.
This ellipse has the center in the midpoint of the segment connecting the vertices. Obviously, the midpoint is the coordinate origin (0,0).
The major semi-axis has the length of 4 units.
So, the ellipse has a canonical equation of the form
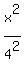 + +  = =  , (1)
where b is an unknown semi-minor axis.
We find b from the condition that the point (2,1) lies on the ellipse, so its coordinates satisfy the equation (1): , (1)
where b is an unknown semi-minor axis.
We find b from the condition that the point (2,1) lies on the ellipse, so its coordinates satisfy the equation (1):
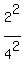 + +  = =  . (2)
Simplify it and solve for b: . (2)
Simplify it and solve for b:
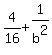 = =  ---> ---> 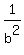 = = 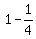 ---> ---> 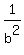 = =  ---> --->  = =  .
Hence, b = .
Hence, b =  = = 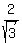 = = 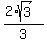 .
Thus the minor semi-axis is b = .
Thus the minor semi-axis is b = 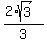 , and the canonical equation of the ellipse is , and the canonical equation of the ellipse is
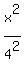 + + 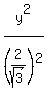 = =  . .
|
|
|
| |