SOLUTION: Calculate the eccentricity e of the ellipse. (Enter your answer in exact form.) Vertices at (4, 7) and (4, -3); c = 1

 



The ellipse looks almost like a circle, but it's a little 
taller than it is wide.

The two black points are the two given vertices, (4,7) and (4,-3),
the green line between the vertices is the major axis, and we can
count that it is 10 units long.  The red point (4,2) is the center.
It is the midpoint of the major axis.  The value of "a", the semi-
major axis is one-half of the major axis 10, therefore the answer
is



That's all you were asked for, but you could have been asked for
the foci (or focal points), the co-vertices, and the equation as well.

The equation of any ellipse with a vertical major axis is 



where (h,k) is the center, a = the semi-major axis, and
b = the semi-minor axis.

The two blue points (4,1) and (4,3) are the foci (or focal points).  
They are the points on the green major axis that are c=1 units from 
the center.

The blue line is the minor axis.  Half its length, called the
semi-minor axis is the value of "b".  The equation that is true 
in every ellipse is that .  Substituting c=1 and 
a=10,  








So the covertices are the endpoints of the minor axis. we get them
by adding and subtracting "b" to/from the x-coordinate of the 
center.  They are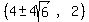 

So the equation



becomes:



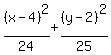Edwin