|
Question 1029039: I was absent the day we studied this and the teacher won't help me out- could you explain how I would do a problem like this?
Use the focus-directrix definition of a parabola to answer the following question
1) How would the shape of the parabola change if the focus were moved up, away from the directrix? How would we describe p?
Answer by josgarithmetic(39618)   (Show Source):
You can put this solution on YOUR website! Try to draw the situation on paper as in sketching a graph. Make one sketch using the definition to form as picture of a parabola. Now make another sketch but MOVE the focus higher than before, and draw this parabola. How has this changed?
Label whatever you can label in the sketches you make, and pay attention to p, which is how far away the vertex of the parabola is from the focus and from the directrix. In the first sketch you have just the value p; but in the second sketch, your focus becomes, for some value d, the distance from THE DIRECTRIX TO THE FOCUS, something+d. In this second case, you should find that the vertex is moved to a y value of 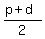 upward from the first sketch.
You said that you missed the lesson on when your teacher gave instruction about the definition of the parabola using focus, directrix, and distance formula. You need to study what your textbook discusses about this; and you should also carefully check these two videos:
derive parabola equation using definition, focus, directrix, and distance formula
derive equation for parabola, but vertex not at the origin
|
|
|
| |
