|
Question 1028394: Could someone please help me with writing a conic equation in standard form for this problem?
1) An ellipse centered at (-2,3) with a major vertical axis 14 units long and a minor axis 6 units long. *my book shows the form of a standard equation for an ellipse with a vertical major axis as x^2/b^2 +y^2/a^2=1, but I don't understand which number goes where?
Thanks for any help!
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the following reference might be able to help you better.
the general formula is:
(x-h)^2 / a^2 + (y-k)^2 / b^2 = 1
they change the names around which can cause quite a confusion.
i usually leave them as is and i get the right answer anyway.
a would represent the horizontal length from the center of the ellipse to the circumference of the ellipse.
b would represent the vertical length from the center of the ellipse to the circumference of the ellipse.
in your equation, you are given that the vertical axis is 14 units long and the horizontal axis is 6 units long.
that would make a = 3 and b = 7.
the center of your ellipse is at (-2,3) which means that h = -2 and k = 3.
the formula of (x-h)^2 / a^2 + (y-k)^2 / b^2 = 1 becomes:
(x+2)^2/3^2 + (y-3)^2/7^2 = 1
simplify this to get:
(x+2)^2 / 9 + (y-3)^2 / 49 = 1
you can graph that equation as is, if your graphing software gives you the capability to do that.
you would get something that looks like the following:
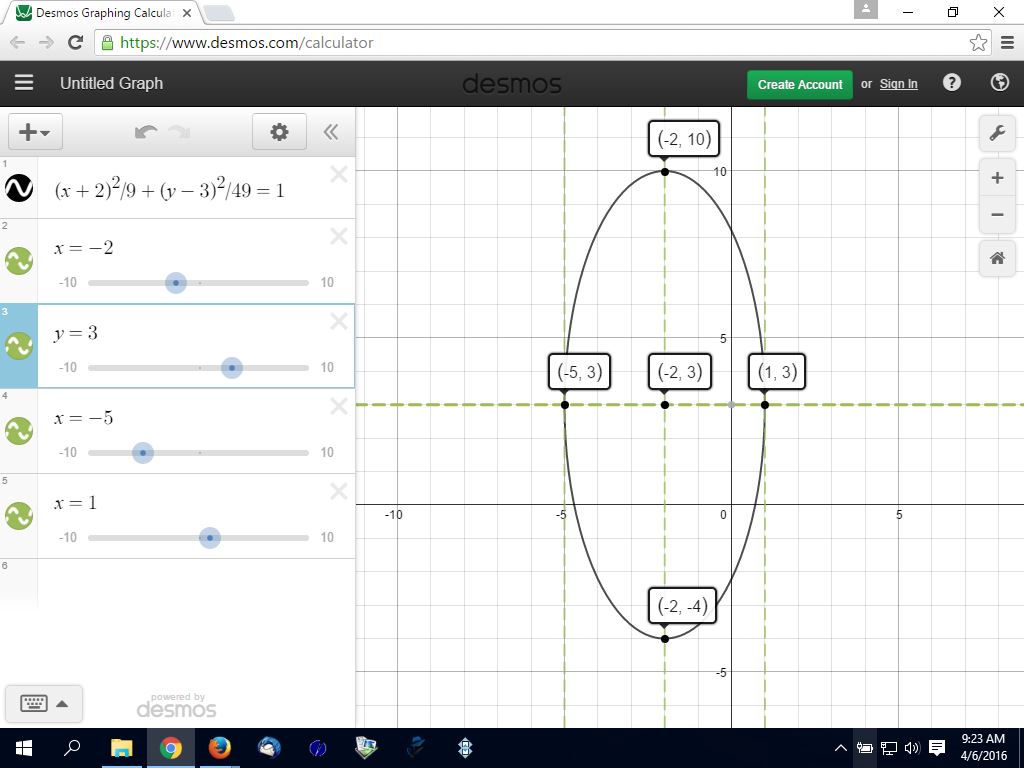
i believe this ellipse satisfies the requirements.
its center is at (-2,3).
its vertical axis is 14 units long.
its horizontal axis is 6 units long.
the really confusing parts of these formulas is what they call a and what they call b.
that changes.
i kept them the same, but if you followed instructions that a is the major axis and b is the minor axis, then your formula would have been:
(y-k)^2 / a^2 + (x-h)^2 / b^2 = 1
this is because, in your problem, the gvertical axis is the major axis and the horizontal axis is the minor axis and a is the major axis and b is the minor axis.
my method, which i've also seen elsewhere, keeps a as the horizontal axis and b as the vertical axis and just uses the formula as is, which i find less confusing, even though it may not be technically correct.
read the reference, which is good, and you'll see the explanation of major and minor axes using a and b there.
that same website has other conics as well such as hyperbola and parabola, which i found useful when i was looking.
|
|
|
| |