SOLUTION: find the equation of the line tangent to the ellipse x^2+3y^2-x+2y=0 at the origin. Thank you!

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: find the equation of the line tangent to the ellipse x^2+3y^2-x+2y=0 at the origin. Thank you!      Log On


   

Question 1024669: find the equation of the line tangent to the ellipse x^2+3y^2-x+2y=0 at the origin. Thank you!
Answer by Edwin McCravy(20059) About Me  (Show Source):
You can put this solution on YOUR website!

This can be done with or without calculus.  I'll do it
both ways since I don't know what math you are taking:

Without using calculus:

Any line through the origin has slope m and y-intercept
(0,0), so its equation is y = mx

If a line is tangent to a curve, the two solutions to
the system of equations of the line and the curve
will be equal.

So we solve the system:

system%28x%5E2%2B3y%5E2-x%2B2y=0%2Cy=mx%29

by substitution and set the discriminant = 0,
so that the two solutions will be the same.

x%5E2%2B3y%5E2-x%2B2y=0
x%5E2%2B3%28mx%29%5E2-x%2B2%28mx%29=0
x%5E2%2B3m%5E2x%5E2-x%2B2mx=0
%281%2B3m%5E2%29x%5E2%2B%28-1%2B2m%29x=0
%281%2B3m%5E2%29x%5E2%2B%28-1%2B2m%29x=0

The discriminant = b%5E2-4ac = 

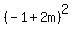%28-1%2B2m%29%5E2-4%28%281%2B3m%5E2%29%2A0%29 =

%28-1%2B2m%29%5E2 =

Set that = 0:

%28-1%2B2m%29%5E2=0 =

-1%2B2m=0

2m=1

m=1%2F2

So slope = m = 1%2F2

Since the y-intercept is (0,0)

y+=+mx+%2B+b  becomes

y=expr%281%2F2%29x

------------------------

Using calculus:

x%5E2%2B3y%5E2-x%2B2y=0

Differentiate implicitly:

2x%2B6y%2A%22y%27%22-1%2B2%2A%22y%27%22=0 

Substitute x=0, y=0

2%280%29%2B6%280%29%2A%22y%27%22-1%2B2%2A%22y%27%22=0

-1%2B2%2A%22y%27%22=0

2%2A%22y%27%22=1

%22y%27%22=1%2F2

So slope = m = 1%2F2

Since the y-intercept is (0,0)

y+=+mx+%2B+b  becomes

y=expr%281%2F2%29x

Edwin