|
Question 1024265: find the center,foci and semi-axes of the ellipse x^2+4y^2=4x+8y
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website! find the center,foci and semi-axes of the ellipse
You need to know the two standard forms of ellipses:
 which is the equation
of an ellipse that looks like this: which is the equation
of an ellipse that looks like this:  and
and
 which is the equation
of an ellipse that looks like this: which is the equation
of an ellipse that looks like this:  We can tell them apart because "a" is always a larger
number than "b".
"a" is the length of the semi-major axis, and "b" is the
length of the semi-minor axis. The center is (h,k). The
vertices are the end points of the major axis. They are
"a" units on each side of the center. The co-vertices are
the end points of the minor axis. They are respectively "a"
and "b" units on each side of the center.
The foci are points on the major axis which are "c" units
on each side of the center, where "c" is calculated by the
formula:
We can tell them apart because "a" is always a larger
number than "b".
"a" is the length of the semi-major axis, and "b" is the
length of the semi-minor axis. The center is (h,k). The
vertices are the end points of the major axis. They are
"a" units on each side of the center. The co-vertices are
the end points of the minor axis. They are respectively "a"
and "b" units on each side of the center.
The foci are points on the major axis which are "c" units
on each side of the center, where "c" is calculated by the
formula:  We must get the equation of an ellipse into one of the above
standard forms:
We must get the equation of an ellipse into one of the above
standard forms:


 To the side, multiply the coefficient of x,
which is -4, by 1/2, which gives -2. Then
square -2 getting +4. Add that inside the
first parentheses and to the right side.
To the side, multiply the coefficient of x,
which is -4, by 1/2, which gives -2. Then
square -2 getting +4. Add that inside the
first parentheses and to the right side.
 Also to the side, multiply the coefficient of y,
which is -2, by 1/2, which gives -1. Then
square -1 getting +1. Add that inside the
first parentheses and to the right side. However
since there is a +4 preceding that parentheses,
adding +1 inside that parentheses is the same as
adding +4 to the left side, so we add +4 to the right
side:
Also to the side, multiply the coefficient of y,
which is -2, by 1/2, which gives -1. Then
square -1 getting +1. Add that inside the
first parentheses and to the right side. However
since there is a +4 preceding that parentheses,
adding +1 inside that parentheses is the same as
adding +4 to the left side, so we add +4 to the right
side:
 We factor each parentheses and combine terms on the
right:
We factor each parentheses and combine terms on the
right:
 Since the factorization results in the products of
a binomial times itself, we can write each as the
square of a binomial:
Since the factorization results in the products of
a binomial times itself, we can write each as the
square of a binomial:
 Next we get 1 on the right side by dividing through by 8
Next we get 1 on the right side by dividing through by 8
 We divide top and bottom of the second fraction
We divide top and bottom of the second fraction  by 4 getting
by 4 getting  . So we have: . So we have:
 Since the denominator 8 under the first term is greater
than the denominator 2 under the second term, we know
that the ellipse looks like this:
Since the denominator 8 under the first term is greater
than the denominator 2 under the second term, we know
that the ellipse looks like this:  We also know that the center is (2,1). We know that
We also know that the center is (2,1). We know that
 and and  , and , and  and and  .
Since we know that .
Since we know that  is approximately 1.4, we have
this graph with the center and the two vertices: is approximately 1.4, we have
this graph with the center and the two vertices:
 We only need to find the two foci. We calculate "c":
We only need to find the two foci. We calculate "c":



 The foci are the two points
The foci are the two points
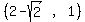 and and 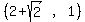 ,
the red points below: ,
the red points below:
 Edwin
Edwin
|
|
|
| |