

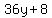 Divide through by 9
Divide through by 9
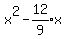

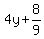
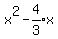

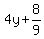 Complete the square:
Complete the square:

 Add to both sides
Add to both sides
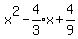

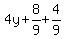
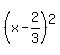

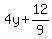
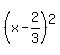

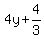
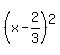

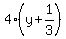
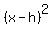

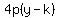 h=2, 4p=4, p=1, k=-1/3
Vertex = (h,k) =
h=2, 4p=4, p=1, k=-1/3
Vertex = (h,k) = 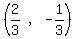 Length of latus rectum = 4p = 4.
p = 1.
Distance from vertex to the focus =
Distance from vertex to the directrix = p = 1
y-coordinate of vertex =
Length of latus rectum = 4p = 4.
p = 1.
Distance from vertex to the focus =
Distance from vertex to the directrix = p = 1
y-coordinate of vertex =  , add p=1, get
, add p=1, get  ,
so focus =
,
so focus =  .
x-coordinate of right endpoint of latus rectum =
x-ccordinate of focus plus half of latus rectum's length,
2p, get
.
x-coordinate of right endpoint of latus rectum =
x-ccordinate of focus plus half of latus rectum's length,
2p, get  x-coordinate of left endpoint of latus rectum =
x-ccordinate of focus minus half of latus rectum's length,
2p, get
x-coordinate of left endpoint of latus rectum =
x-ccordinate of focus minus half of latus rectum's length,
2p, get  y-coordinates of ends of latus rectum = same as y-coordinate
of focus,
y-coordinates of ends of latus rectum = same as y-coordinate
of focus,  right end of latus rectum =
right end of latus rectum = 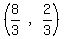 right end of latus rectum =
right end of latus rectum = 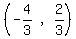 Directrix has equation y = y-coodinate of vertex minus p = 1
which is
Directrix has equation y = y-coodinate of vertex minus p = 1
which is  Directrix has equation
Directrix has equation  blue line segment is latus rectum
green line is directrix
Upper point marked is focus
Lower point marked is vertex
blue line segment is latus rectum
green line is directrix
Upper point marked is focus
Lower point marked is vertex
 Edwin
Edwin