Question 1010722: worlds of fun is designing a new ride the ride has 2 tracks that are hyperbolic if the ride is placed on a coordinate grid the vertices of the ride are at (-3,2) and (5,2) and the foci are at (-5,2) and (7,2)
explain how to find the values of A,B, and C for the hyperbolic tracks and state their values
Answer by FormerJosephStalin(2)   (Show Source):
You can put this solution on YOUR website! Hi, Thanks for the question.
So the hyperbola has vertices of (-3,2) and (5,2). Since both of the vertices both have the same y-coordinate, this is going to be a horizontal hyperbola. The a-value of the hyperbola represents the distance from the center to the vertices. In order to calculate the center, it is simply the midpoint between the two vertices.
Recall the midpoint formula
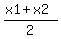 So we would so (-3+5)/2 to get our x-coordinate which is 1 and (2+2)/2 to get the y-coordinate of the midpoint which is 2. So the center is (1,2). Since a is the distance between the center and vertices, in this case since (-3,2) is 4 units from (1,2) and (1,2) is 4 units from (5,2). The a-value is 4.
The c value is the distance from the center to the foci, so (1,2) is 6 units from (7,2) and (1,2) is also 6 units from (-5,2). So c is 6.
Remember that  is used to find the foci hyperbola. Since we now know a and c, we can find b. So we will substitute the values into the equation. 4^2+b^2=6^2 So 16 + b^2 = 36 Solving for b, we get the  or 2* .
In conclusion, a = 4, b = 2* and c = 6
Hope this helped :) Have a good day!
|
|
|
