|
Question 982017: A building has an entry the shape of a parabolic arch 22 ft high and 28 ft wide at the base as shown below.
Find an equation for the parabola if the vertex is put at the origin of the coordinate system.
Answer by josmiceli(19441)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let the equation of the arch be:

where 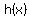 is the vertical location is the vertical location
of any point ( x,h ) on the arch.
and 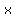 is the horizontal location is the horizontal location
of any point ( x,h ) on the arch
-------------------------------
The formula for the x-coordinate of the
vertex is:

Since the vertex is at the origin,


So, now the equation is:

Plugging in the point ( 0-,0 ), I get

so, 
Now the equation is:

-----------------------
I am given the points:
( 14, -22 ) and
( -14, -22 )
----------------



and



--------------------
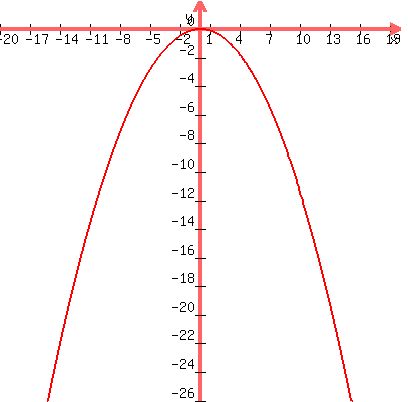
The equation is:

------------------------
check:
does it go through ( 14, -22 ) and ( -14, -22 ) ?



You can check the other point ( -14, -22 )
Here's the plot:
|
|
|
| |