The trouble with parabolas is that different books use different notation.
They are all equivalent, but they are just different enough to cause confusion.
I will arbitrarily pick one of the notations. If your book is different, just
tell me what your book gives for the standard equation for a parabola in the
thank-you note below and I'll change it on here to fit your notation. One
common one is:
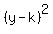
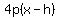where (h,k) = the vertex, p is the distance from center to focus, positive
if parabola opens right and negative if it opens left.
We plot the focus point and draw the the directrix, a vertical line
through x=-2 on the x-axis:
The vertex is a point exactly half-way between the focus and the directrix
line. That is the point (h,k) = (1,7)
p = the distance from the center to the focus is 3 units here.
The focal chord (sometimes called the latus rectum) is a line which is 4p
units long (in this case 4*3 or 12 units long) bisected at the focus. So
it's 6 units up from the focus and 6 units down from the focus:
And now we can sketch the parabola:
h=1,k=7, 4p = 12, so the equation is
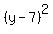
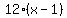Edwin
