Question 936512: What are the coordinates of the center, the lengths of the major and minor axes, vertices, co-vertices, and foci for each ellipse:
x^2/9 + y^2/16 =1
Found 2 solutions by lwsshak3, MathLover1:
Answer by lwsshak3(11628)   (Show Source): (Show Source):
You can put this solution on YOUR website! What are the coordinates of the center, the lengths of the major and minor axes, vertices, co-vertices, and foci for each ellipse:
x^2/9 + y^2/16 =1
Given ellipse has a vertical major axis:
Its standard form of equation:  , a>b, (h,k)=coordinates of center , a>b, (h,k)=coordinates of center
..
For given ellipse:
center:(0,0)
a^2=16
a=4
length of major axis=2a=8
b^2=9
b=3
length of minor axis=2b=6
vertices:(0,0±a)=(0,0±4)=(0,-4) and (0,4)
co-vertices:(0±b,0)=(0±3,0)=(-3,0) and (3,0)
foci:
c^2=a^2-b^2=16-9=7
c=√7≈2.6
foci:(0,0±c)=(0,0±2.6)=(0,-2.6) and (0,2.6)
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! The standard form of the equation of an ellipse is:
 for horizontal ellipses, and for horizontal ellipses, and
 for vertical ellipses for vertical ellipses
In these equations, the " " and the " " and the " " are the " are the  and and  coordinates, respectively, of the center. coordinates, respectively, of the center.
here is your ellipse:

from given we know that  , ,  ; so, center is at origin ( ; so, center is at origin ( , , ) )
we also know that major axis is vertical and
semi-major axis length is 
semi-minor axis length is 
the vertices will be " " distance above and below the center: " distance above and below the center:
vertices ( , ,  ) | ( ) | ( , , ) )
The co-vertices are right and left:
( , , ) | ( ) | ( , , ) )
The distance from the center to each focus is called " ". The " ". The " " is not in the standard form of the equation for an ellipse. But there is a fixed relationship between the " " is not in the standard form of the equation for an ellipse. But there is a fixed relationship between the " ", the " ", the " " and the " " and the " " values: " values:





foci: | ( , ,  ) | ( ) | ( , ,  ) )
or approximately ( , , 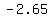 ) | ( ) | ( , ,  ) )

|
|
|