Question 930815: Find the vertices, foci, and eccentricity of the ellipse. Determine the lengths of the major and minor axes, and sketch the graph.
1. 4x^2+25y^2=100
2. x^2/16+y^2/25=1
3. 1/2x^2+1/8y^2=1/4
4. y^2=1-2x^2
5. X^2+4y^2=16
Answer by ewatrrr(24785)   (Show Source): (Show Source):
You can put this solution on YOUR website! Standard Form of an Equation of an Ellipse is 
where Pt(h,k) is the center. (a variable positioned to correspond with major axis)
a and b are the respective vertices distances from center.
The foci distances from center: c = ±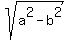 where a > b where a > b
eccentricity = c/a
.........
4x^2+25y^2=100
 C(0,0) C(0,0)
V(5,0),V(-5,0) & V(0,2),V(0,-2)
c =√(25 - 4) = √(21)
eccentricity = √21/5

..........
x^2/16+y^2/25=1
 C(0,0) C(0,0)
& V(4,0),V(-4,0) & V(0,5),V(0,-5)
c =√(25 - 16) = 3
eccentricity = 3/5

........
1/2x^2+1/8y^2=1/4
2x^2 + y^2/4 = 1

.........
y^2=1-2x^2
2x^2 + y^2 = 1

.......
X^2+4y^2=16

|
|
|