I'm trying to read your mind.
I will guess that the red line is the semi-minor-axis, b.
I will guess that the blue line you want to find connects the top
(co-vertex) to a focal point (or focus).
The semi-major axis is  of the major axis, a, so a =
of the major axis, a, so a =  .
.
 First we find c, which is the distance from the center to the focus.
All elipses have the property
c² = a² - b²
c² =
First we find c, which is the distance from the center to the focus.
All elipses have the property
c² = a² - b²
c² = 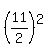 - 4²
c² =
- 4²
c² = 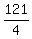 - 16
c² =
- 16
c² = 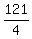 -
-  c² =
c² = 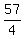 By the Pythagorean theorem,
(blue line)² = c² + b²
(blue line)² =
By the Pythagorean theorem,
(blue line)² = c² + b²
(blue line)² = 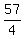 + 4²
(blue line)² =
+ 4²
(blue line)² = 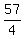 +
+  (blue line)² =
(blue line)² = 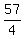 +
+  (blue line)² =
(blue line)² = 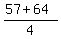 (blue line)² =
(blue line)² = 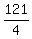 blue line =
blue line = 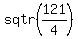 blue line =
blue line =  So the blue line is equal to the semi-major axis.
Edwin
So the blue line is equal to the semi-major axis.
Edwin