Question 726805: The semi-major axis has length 2root13 units, and the foci are at (-1,1) and (-1,-5).
Write the equation of the ellipse that meets each set of conditions.
Answer by lwsshak3(11628)   (Show Source):
You can put this solution on YOUR website! The semi-major axis has length 2root13 units, and the foci are at (-1,1) and (-1,-5).
Write the equation of the ellipse that meets each set of conditions.
***
Standard form of equation for an ellipse with vertical major axis:
 , a>b, (h,k)=(x,y) coordinates of center
For given ellipse:
center:(-1,-2)
a=2√13
a^2=4*13=52
c=3 (from center to foci)
c^2=9
c^2=a^2-b^2
b^2=a^2-c^2=52-9=43
Equation of given ellipse:
|
|
|
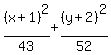
