Those are all equations of circles and they are all done the same way,
I'll do the 2nd one as it is the most complete and the 3rd one is weird:
2. 36x²+36y²+36y=48x+199
Get the x-term next to the x² term and the y-term next to the y² term.
Get only the constant term on the right.
36x²-48x + 36y² + 36y = 199
Divide every term through by the common coefficient of the x²
and the y² terms, which is 36
x² - 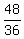 x + y² + y =
x + y² + y =  Reduce the fraction
Reduce the fraction 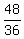 to
to  x² -
x² -  x + y² + y =
x + y² + y =  Complete the squares on the lft:
1. Multiply the coefficient of x, which is
Complete the squares on the lft:
1. Multiply the coefficient of x, which is  , by
, by  ,
getting
,
getting  .
2. Square this result, getting
.
2. Square this result, getting 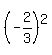 =
=  3. Add this right after the x term on the left side and also
add it to the right side.
1. Multiply the coefficient of y, which is 1, by
3. Add this right after the x term on the left side and also
add it to the right side.
1. Multiply the coefficient of y, which is 1, by  ,
getting
,
getting  .
2. Square this result, getting
.
2. Square this result, getting  =
=  3. Add this right after the y term on the left side and also
add it to the right side.
x² -
3. Add this right after the y term on the left side and also
add it to the right side.
x² -  x +
x +  + y² + y +
+ y² + y +  =
=  +
+  +
+  Factor the first three terms as (x -
Factor the first three terms as (x -  )(x -
)(x -  ) which can be
written as the square (x -
) which can be
written as the square (x -  )².
Factor the last three terms on the left as (y -
)².
Factor the last three terms on the left as (y -  )(y -
)(y -  ) which can be
written as the square (y -
) which can be
written as the square (y -  )².
Combine the terms on the right by getting an LCD of 36
)².
Combine the terms on the right by getting an LCD of 36
 +
+  +
+  =
=  +
+ 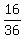 +
+ 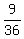 =
= 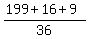 =
= 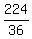 =
= 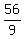 (x -
(x -  )² + (y -
)² + (y -  )² =
)² = 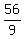 That is a circle with center (
That is a circle with center ( ,
, ) and radius
) and radius 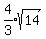 .
----------------------------------
9x²+9y²+6x=-5
Get the x-term next to the x² term and the y-term next to the y² term.
The constant term is already on the right.
9x² + 6x + 9y² = -5
Divide every term through by the common coefficient of the x²
and the y² terms, which is 9:
x² -
.
----------------------------------
9x²+9y²+6x=-5
Get the x-term next to the x² term and the y-term next to the y² term.
The constant term is already on the right.
9x² + 6x + 9y² = -5
Divide every term through by the common coefficient of the x²
and the y² terms, which is 9:
x² -  x + y² =
x + y² = 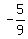 Reduce the fraction
Reduce the fraction  to
to  x² -
x² -  x + y² =
x + y² = 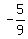 Complete the squares on the left:
1. Multiply the coefficient of x, which is
Complete the squares on the left:
1. Multiply the coefficient of x, which is  , by
, by  ,
getting
,
getting  .
2. Square this result, getting
.
2. Square this result, getting 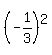 =
=  3. Add this right after the x term on the left side and also
add it to the right side.
Since there is no y term, write y² as (y - 0)²
x² -
3. Add this right after the x term on the left side and also
add it to the right side.
Since there is no y term, write y² as (y - 0)²
x² -  x +
x +  + (y - 0)² =
+ (y - 0)² = 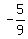 +
+  Factor the first three terms as (x -
Factor the first three terms as (x -  )(x -
)(x -  ) which can be
written as the square (x -
) which can be
written as the square (x -  )².
Combine the terms on the right:
)².
Combine the terms on the right:
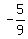 +
+  =
=  (x -
(x -  )² + (y - 0)² =
)² + (y - 0)² =  That is an imaginary circle with a real center of (
That is an imaginary circle with a real center of ( ,0) and an imaginary
radius of
,0) and an imaginary
radius of  i. Really weird. Was that -5 on the right supposed to be 5?
Edwin
i. Really weird. Was that -5 on the right supposed to be 5?
Edwin
----------------------------------