|
Question 608548: Write the equation in standard form for the conic section.
An ellipse centered at (3,2) with vertices at (9,2) and (-3,2)and co vertices at (3,5) and (3,-1)
Found 2 solutions by solver91311, Edwin McCravy:
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website!
From the coordinates of the center and the vertices/co-vertices, we can see that the center is at (3,2), the semi-major axis measures 6 (because the distance from (3,2) to (9,2) is 6) and the semi-minor axis measures 3 (because the distance from (3,2) to (3,5) is 3). Furthermore the major axis is parallel to the  -axis (because the line through (3,2) and (9,2) is horizontal). -axis (because the line through (3,2) and (9,2) is horizontal).
The equation of an ellipse centered at ) with a semi-major axis that measures with a semi-major axis that measures  , a semi-minor axis that measures , a semi-minor axis that measures  , and a major axis parallel to the , and a major axis parallel to the  -axis is: -axis is:
^2}{a^2}\ +\ \frac{(y\ -\ k)^2}{b^2}\ =\ 1)
Just plug in the numbers.
John

My calculator said it, I believe it, that settles it
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website! Write the equation in standard form for the conic section.
An ellipse centered at (3,2) with vertices at (9,2) and (-3,2)and co vertices at (3,5) and (3,-1)
I think you need a more graphical approach than just a word explanation.
Plot the points and draw the graph:
 Since the ellipse is this way "
Since the ellipse is this way " " and not this way " " and not this way " ", its equation is: ", its equation is:
 + +  = 1
[Had it been the other way the "a" and "b" would be switched. In an
ellipse "a" is always larger than "b", but not necessarily in a hyperbola!]
(h,k) = the center = (3,2), "a" = semi-major-axis, sometimes called
"the long radius" and "b" = the semi-minor-axis, sometimes called
"the short radius".
draw the semi-major and semi-minor axes:
The red line is the semi-major axis and the green line is the semi-minor
axis. = 1
[Had it been the other way the "a" and "b" would be switched. In an
ellipse "a" is always larger than "b", but not necessarily in a hyperbola!]
(h,k) = the center = (3,2), "a" = semi-major-axis, sometimes called
"the long radius" and "b" = the semi-minor-axis, sometimes called
"the short radius".
draw the semi-major and semi-minor axes:
The red line is the semi-major axis and the green line is the semi-minor
axis.
 Count the number of units that the red and green lines are in
length and you'll get a = 6 and b = 3. Therefore the equation
Count the number of units that the red and green lines are in
length and you'll get a = 6 and b = 3. Therefore the equation
 + +  = 1
becomes: = 1
becomes:
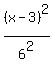 + + 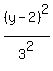 = 1
or = 1
or
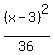 + + 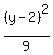 = 1
Edwin = 1
Edwin
|
|
|
| |