Question 528281: how do i write an equation for a hyperbola with the give information, vertices (-4,0) (4,0) conjugate axis length of 8
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website! how do i write an equation for a hyperbola with the give information, vertices (-4,0) (4,0) conjugate axis length of 8
The transverse axis is the line segment between the vertices (-4,0) and
(4,0) which is 8 units long. Its midpoint is the origin. The transverse
axis is horizontal so the equation is of the form:
 - -  = 1
where a = one-half the transverse axis, which is half of 8 or 4, and
where b = one-half the conjugate axis, which is half of 8 or 4, so
a and b are both 4, so the equation is = 1
where a = one-half the transverse axis, which is half of 8 or 4, and
where b = one-half the conjugate axis, which is half of 8 or 4, so
a and b are both 4, so the equation is
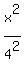 - - 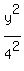 = 1 = 1
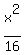 - - 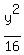 = 1
That's the standard form, or you can clear of fractions and get
x² - y² = 16
Edwin = 1
That's the standard form, or you can clear of fractions and get
x² - y² = 16
Edwin
|
|
|