|
Question 455974: I have to find the center, vertices, co-vertices, foci, and asymptotes for the hyperbola  . Can someone help me please? . Can someone help me please?
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
4x² - 8x - y² + 4y - 4 = 0
Factor the coefficient of x², which is 4, out of
the two x-terms
4(x² - 2x) - y² + 4y - 4 = 0
Factor the coefficient of y², which is -1, out of
the two y-terms
4(x² - 2x) - (y² - 4y) - 4 = 0
Get the term -4 off the left side by adding
4 to both sides:
4(x² - 2x) - (y² - 4y) = 4
Multiply the coefficient of x inside the parentheses,
which is -2 by ½ getting -1. Then square -1 getting +1.
Add +1 inside the first parentheses, and offset it by
adding +4 to the right side, since adding +1 inside
the first parentheses amounts to adding +4 to the left side
because of the 4 outside the first parentheses:
4(x² - 2x + 1) - (y² - 4y) = 4 + 4
Combine the 4 + 4 on the right as 8
4(x² - 2x + 1) - (y² - 4y) = 8
Multiply the coefficient of y inside the second parentheses,
which is -4 by ½ getting -2. Then square -2 getting +4.
Add +4 inside the second parentheses, and offset it by
adding -4 to the right side, since adding +4 inside
the second parentheses amounts to adding -4 to the left side
because of the - outside the second parentheses:
4(x² - 2x + 1) - (y² - 4y + 4) = 8 - 4
Combine the 8 - 4 on the right as 4
4(x² - 2x + 1) - (y² - 4y + 4) = 4
Factor x² - 2x + 1 as (x - 1)(x - 1) and then as (x - 1)²
Factor y² - 4y + 4 as (y - 2)(y - 2) and then as (y - 2)²
4(x - 1)² - (y - 2)² = 4
Next we must get a 1 on the right.
So we divide all the terms by 4
4(x - 1)² (y - 2)² 4
————————— - ———————— = ———
4 4 4
(x - 1)² (y - 2)²
————————— - ———————— = 1
1 4
Next we compare that to
(x - h)² (y - k)²
————————— - ———————— = 1
a² b²
which means that it is a hyperbolka that looks like this )(
We see that h = 1, k = 2, a² = 1 so a = 1 and b² = 4 so b = 2
The center = (h,k) = (1,2)
Plot the center (1,2)
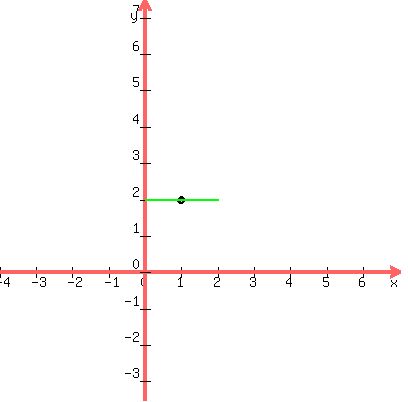
 Draw the transverse axis which is 2a or 2 units long and
is horizontal, with the center at its midpoint. That
means we draw 1 units left of the center and 1 units
right of the center to get the complete transverse
axis, drawn in green below:
Draw the transverse axis which is 2a or 2 units long and
is horizontal, with the center at its midpoint. That
means we draw 1 units left of the center and 1 units
right of the center to get the complete transverse
axis, drawn in green below:
 Next draw the conjugate axis which is 2b or 4 units long and
is vertical, with the center at its midpoint. That
means we draw 2 units up from the center and 2 units
down from the center to get the complete transverse
axis, also drawn in green below:
Next draw the conjugate axis which is 2b or 4 units long and
is vertical, with the center at its midpoint. That
means we draw 2 units up from the center and 2 units
down from the center to get the complete transverse
axis, also drawn in green below:
 Next we draw the defining rectangle, which is a
rectangle with the ends of the transverse and
conjugate axes as midpoints of the sides. I'll
draw it in green, too:
Next we draw the defining rectangle, which is a
rectangle with the ends of the transverse and
conjugate axes as midpoints of the sides. I'll
draw it in green, too:
 Next we draw the extended diagonals of the defining rectangle.
They will be the asymptotes of the hyperbola:
Next we draw the extended diagonals of the defining rectangle.
They will be the asymptotes of the hyperbola:
 Now we can sketch in the hyperbola to have its vertices as
the ends of the transverse axis and to approach the \
asymptotes. I'll draw the hyperbola in red:
Now we can sketch in the hyperbola to have its vertices as
the ends of the transverse axis and to approach the \
asymptotes. I'll draw the hyperbola in red:
 vertices, co-vertices, foci, and asymptotes
The vertices are the endpoints of the transverse axis.
They are (0,2) and (2,2)
The co-vertices are the endpoints of the conjugate axis.
They are (1,0) and (1,4)
To find the foci we calculate c from the formula
c² = a² + b²
c² = 1² + 2²
c² = 1 + 4
c² = 5_
c = √5
Then the foci are the points which are c units right
and left of the vertices. They are
_ _
(1+√5,2) and (1-√5,2)
I'll plot the two foci:
vertices, co-vertices, foci, and asymptotes
The vertices are the endpoints of the transverse axis.
They are (0,2) and (2,2)
The co-vertices are the endpoints of the conjugate axis.
They are (1,0) and (1,4)
To find the foci we calculate c from the formula
c² = a² + b²
c² = 1² + 2²
c² = 1 + 4
c² = 5_
c = √5
Then the foci are the points which are c units right
and left of the vertices. They are
_ _
(1+√5,2) and (1-√5,2)
I'll plot the two foci:
 Now all we need are the equations of the two asymptotes:
The asymptote that slants uphill to the right passes through (0,0)
and (1,2),
We use the slope formula
Now all we need are the equations of the two asymptotes:
The asymptote that slants uphill to the right passes through (0,0)
and (1,2),
We use the slope formula  Substitute in
Substitute in 
 y = 2x
That's the equation of the asymptote that slants
uphill to the right.
The asymptote that slants downhill to the right
passes through (2,0) and (1,2),
Using the slope formula
y = 2x
That's the equation of the asymptote that slants
uphill to the right.
The asymptote that slants downhill to the right
passes through (2,0) and (1,2),
Using the slope formula  Substitute in
Substitute in 

 y = -2x + 2
That's the equation of the asymptote that slants
downhill to the right.
Edwin
y = -2x + 2
That's the equation of the asymptote that slants
downhill to the right.
Edwin
|
|
|
| |